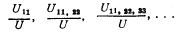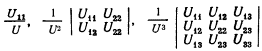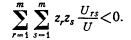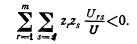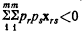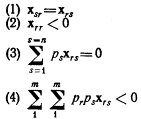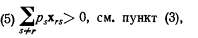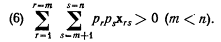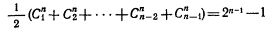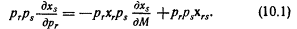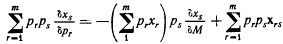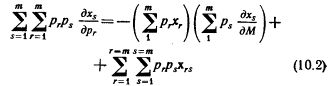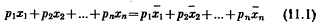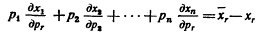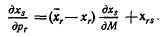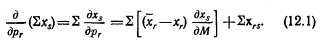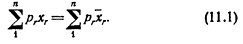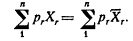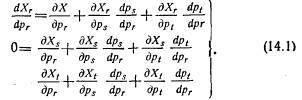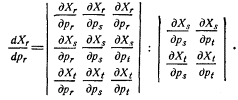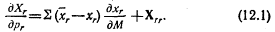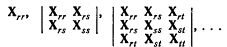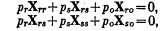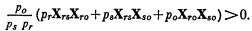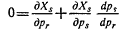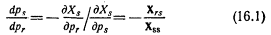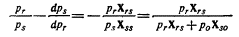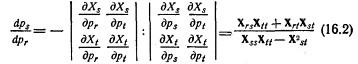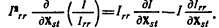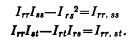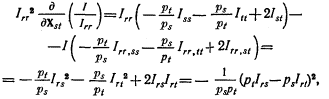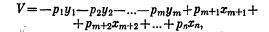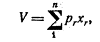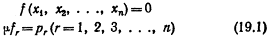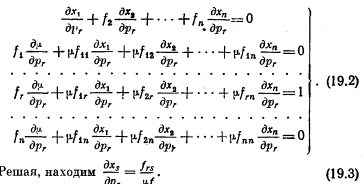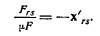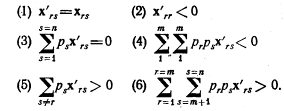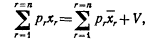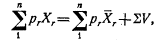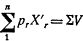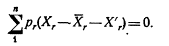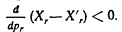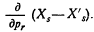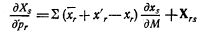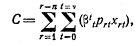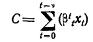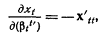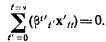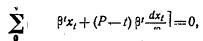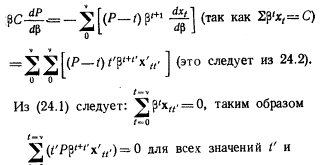1. Цель данных приложений заключается не просто в том, чтобы выразить основные положения, содержа­щиеся в книге, с помощью математических символов - в этом я не вижу особой пользы. Если словесные (или геометрические) рассуждения убедительны, они ничего не выиграют от представления в иной форме. Чего мы мо­жем достигнуть, однако, так это уверенности в том, что наши положения обладают максимально возможной общ­ностью: доказанное для двух, трех или четырех товаров справедливо и для n товаров. В этих приложениях я со­средоточу внимание на доказательстве обоснований та­кого рода обобщений.

Я буду придерживаться того же порядка рассмотре­ния вопросов, что и в тексте книги, и буду выделять ча­сти приложений таким образом, чтобы они соответствовали главам книги, с которыми связаны. Я должен на­чать, однако, с обсуждения чисто математического утвер­ждения, которое играет основную роль в последующем изложении. Какое отношение оно имеет к делу, станет ясно почти сразу.

2. Основное математическое утверждение. (1) Одно­родную функцию второго порядка от трех переменных

ax²+ by² + cz² + 2fyz+ 2gzx+ 2hxy

можно записать также в следующем виде:

Так как переменные появляются только в скобках, а каж­дая скобка возведена в квадрат, сразу ясно, что исходное выражение положительно для всех действительных значений переменных, если коэффициенты при всех скоб­ках положительны, и отрицательным, если все соответст­вующие коэффициенты отрицательны. Эти коэффициенты являются отношениями определителей

Таким образом, исходное выражение будет всегда поло­жительным, если все три определителя положительны; оно будет всегда отрицательным, если первый и третий опре­делители отрицательны, а второй положителен.

(2) Такое же утверждение можно установить для произвольного числа переменных [См.: Burnside and Panto n. Theory of Equations, vol. II, p. 181-182. (По этим вопросам см. также: Р. Беллман. Введение в теорию матриц, гл. 5. М., 1976. - Прим. перев.)]. Квадратичная форма общего вида

a₁₁x²₁+ a₂₂x²₂+...+ a_nnx²_n + 2a₁₂x₁x₂+ 2a₁₃x₁x₃+...+ 2а₂₃x₂x₃+...

будет положительно определена для всех действительных значений х, если определители

все положительны; она будет отрицательно определена, если они отрицательны и положительны попеременно.

(3) Когда требуется найти условия, при которых рас­смотренная выше квадратичная форма положительно или отрицательно определена не для всех значений перемен­ных, а только удовлетворяющих линейному ограничению

b₁x₁+ b₂x₂+ ...+ b_nx_n = 0,

то мы можем двигаться дальше, удалив одну из перемен­ных, например, x₁. Квадратичная форма тогда примет сле­дующий вид:

c₂₂x₂₂ + c₃₃x₃₂ + ...+ c_nnx_n2 + 2с₂₃x₂x₃+ ...,

где

Теперь искомые условия можно тогда записать в той же форме, что и в пункте (2) выше - с с вместо а; их можно упростить, умножить каждый определитель на отрицательную величину (-У). Например:

что получается при добавлении первых двух столбцов с соответствующими множителями к каждому из остав­шихся столбцов.

Таким образом, условие, согласно которому квадратич­ная форма положительно определена при линейном огра­ничении, состоит в том, что определители

должны быть все отрицательны (так как отрицательный множитель -b₁² изменит все знаки); условие, согласно которому она отрицательно определена, состоит в том, что определители должны быть положительными и отри­цательными попеременно.

Это все, что нам нужно из чисто математических основ; теперь обратимся к экономике.

Приложение к главе I

3. Равновесие потребителя. Мы начинаем с рассмот­рения поведения индивида, который располагает фикси­рованной суммой денег М для расходов (назовем эту сум­му условно его «доходом») и имеет возможность потра­тить эту сумму на n различных товаров. Цены этих n то­варов заданы рынком. Обозначим эти цены как p₁, p₂, р₃, ... р_n. Обозначим через x₁, x₂, х₃, ... x_n количества соот­ветствующих товаров, которые индивид покупает.

Тогда, при условии, что он потратит весь свой доход, мы получим:

Предположим пока, что потребности индивида выра­жаются известной функцией полезности u (x₁, х₂, х₃,... x_n). Количество закупленных товаров будет определено из ус­ловия, согласно которому и максимальна при соблюде­нии (3.1). Это количество можно найти, вводя множитель Лагранжа р, и максимизируя выражение:

Условия равновесия потребителя состоят, следовательно, в том. что

где u_r - вписано вместо θu/θx_r - предельной полезности x_r. Таким образом, полученное уравнение выражает ра­венство между предельной полезностью x_r и ценой x_r, умноженной на μ (последний множитель связывается с маршаллианским понятием предельной полезности).

Если избавиться от μ в уравнениях (3.2), то они сво­дятся к виду:

Эти n-1 уравнение вместе с уравнением (3.1) дают n уравнений для определения n количеств: х₁, х₂, ..., x_n.

4. Условия стабильности. Чтобы функция u действительно имела максимум, необходимо, чтобы выполнялось не только du=0 (как показано выше), но и d²u<0. Рас­крывая эти выражения и обозначая как urs вторые частные производные (так же как и ur-первые), получим:

Последнее выражение является квадратичной формой, по­добной той, что мы рассмотрели в § 2 (так как u_s^r=u_rs); следовательно, условие, согласно которому d²u<0 для всех значений dx₁, dx₂, ..., dx_n, таких, что du=0 [Имеется в виду, что изменения х не должны приводить к нарушению бюджетного ограничения (3.1), т. е. Σ p_rdxr=0. Отсюда, с учетом (3.2), получаем, что du=Σu_rdxr=0. - Прим. перев.], состоит в том, что определители

должны быть положительными и отрицательными попе­ременно.

Эти определители будут играть чрезвычайно важную роль в нашем последующем анализе. Я обозначу послед­ний из них как U, а алгебраические дополнения элемен­тов u_r, u_s, u_rr, u_rs в U - как U_r, U_s, U_rr, U_rs. Так как n то­варов могут быть взяты в любом порядке, то из (4.1) не­посредственно следует, что U_rr/U должно быть отрица­тельным.

5. Ординалистский характер полезности. Условия равно­весия и условия стабильности для индивидуального потре­бителя соответствуют предположению, что существует оп­ределенная функция полезности и. Это в действительности самый удобный способ записи таких условий. Важно лишь отметить, что они не зависят от существования какой-либо единственной функции полезности. Так, предположим, что функция полезности и заменяется на любую произвольную функцию от себя самой φ (u). Тогда можно показать, что при соблюдении единственного условия, согласно ко­торому функция φ (u) возрастает с ростом u (т. е. при ус­ловии, что φ '(u) положительна), условия равновесия и условия стабильности при замене функции полезности ни­как не изменяется.

Так как j/jxr φ (u) = φ '(u) ur то условия равновесия (3.3) останутся неизменными. Равные друг другу отношения просто помножаются на общий множитель φ '(u), который можно сократить. (Даже если они записаны в виде (3.2), они все же не изменяются, если μ заменить на φ '(u) μ. Так как μ - произвольно, то такая замена обоснованна.)

Так как (δ²/ δ x_r δ x_s) φ (u) =φ '(u) u_rs+ φ ''(u) u_r u_s то определители из условий устойчивости преобразуются аналогичным образом.

Первый определитель превращается в

подобное преобразование можно произвести с каждым определителем в данной последовательности, r-ый определитель имеет (r+ 2) строк и столбцов; следовательно его придется помножить на множитель {φ '(u)} ^r+2. Так как φ '(u) предполагается положительной, ни один из определителей с введением такого множителя не изменит знак; так как именно знаки определителей связаны со стабильностью, можно считать, что соответствующие условия не изменились при замене и на φ (u).

Таким образом, если мы решим начать (что, я считаю, нам и следует сделать) не с данной функции полезности, а с данной шкалы предпочтений, нам придется лишь сосредоточить внимание на тех свойствах функций полезности, которые инвариантны относительно замены u на φ (u). Исходные условия равновесия и исходные условия стабильности, как было показано, инвариантны относительно такой замены. В остальном наша теория стоимости будет разрабатываться с использованием только инвариантных свойств, хотя, как правило, я буду остав­лять возможность самому читателю проверить инвариантность.

Приложение к главам II и III

6. Влияние увеличения дохода на спрос. Преобразуем уравнения (3.1) и (3.2), записав их в форме:

Возьмем частную производную по М:

Решая, получим

Из (6.1) находим: p_s=u_s/μ, так что это можно записать в виде:

О знаке U_r ничего не известно, следовательно, δx_r/δМ мо­жет быть как положительным, так и отрицательным. (См. гл. II.)

7. Последствия изменения цены при постоянном уров­не дохода. Предположим теперь, что рг меняется, а ос­тальные цены (а также М) неизменны. Из (6.1) имеем:

Решая и упрощая, как и прежде, получим:

Используя (6.3), это можно записать в виде:

Это уравнение, полученное первоначально Слуцким, мож­но считать Основным Уравнением Теории Стоимости. Она показывает, как изменение цены товара x_r воздействует на спрос индивида на другой товар (х_s); это воздействие состоит из двух частей, которые мы назвали эффектом дохода и эффектом замещения соответственно. Так как x_r=dM/dp_r (если М не фиксировано, а все х и все про­чие р фиксированы), то из уравнения следует, что член, соответствующий эффекту замещения, выражает воздей­ствие на спрос на товар x_s изменения цены x_r совместно с таким изменением дохода, которое позволило бы потре­бителю при желании купить то же самое количество то­вара, что и раньше, несмотря на изменение р_r. Очевидно, что изменение дохода будет тем меньше, чем меньшую роль играет x_r в бюджете потребителя.

Полагая, что r=s (а у нас нет причин, которые не позволяли бы нам так считать), то же уравнение можно использовать для разделения воздействия цены х_r на спрос на сам товар x_r. Уравнение примет тогда вид:

Из условий стабильности непосредственно следует, что член уравнения, соответствующий эффекту замещения, должен быть отрицательным.

8. Свойства члена, соответствующего эффекту замещения. В остальном теория спроса состоит по большей ча­сти из выявления свойств этого фундаментального урав­нения. Прежде всего, удобнее переписать его в другой форме. Член μ U_rs/U, соответствующий эффекту замеще­ния, в действительности инвариантен относительно заме­ны u на φ (u) в качестве функции полезности, следова­тельно, лучше записать его в такой форме, при которой уравнение не будет иметь прямой связи с определенной функцией полезности. Поэтому я буду писать его в ней­тральной форме (x_rs), так что уравнения будут иметь вид:

Это как раз такая форма, в которой нам будет наиболее удобно использовать уравнение в дальнейшем [С некоторых точек зрения (я думаю, не все так считают) есть определенный смысл в том, чтобы выражать фундаментальное уравнение в форме эластичностей, что нетрудно сделать, домножив уравнение на p_r/x_s, и сгруппировав полученные выражения в эле­менты, не зависящие от единиц измерения. В моей французской брошюре La Theorie mathematiqae de la Valeur (Hermann 1937) изложены по большей части последующие рассуждения, с исполь­зованием представления в форме эластичностей. Таким образом, читатель сам может сделать выбор.].

Два свойства члена уравнения, соответствующего эф­фекту замещения, сразу следуют из того, что уже сказа­но. Вначале я выпишу эти свойства, а потом выведу и некоторые другие.

(1) Так как оба определителя U_rs и U симметричны по r и s, то x_rs тоже симметричен. Это означает, что x_sr=x_rs. Таким образом, члены, соответствующие эффекту замещения в δх_s/δр_r и δх_r/δр_s, тождественны. Но члены, соответствующие эффекту дохода, вообще говоря, не рав­ны друг другу. Значит, для того чтобы δх_s/δр_r и δх_r/δр_s были равны, необходимо равенство x_rδх_s/δМ и x_sδх_r/δр_r. Это предполагает, что (М/x_r) δх_r/δМ должно быть равно (М/x_s) δх_s/δМ, т. е. эластичность спроса на x_r и эластичность спроса на x_s по отношению к доходу должна быть одинаковой.

(2) Так как U_rr/U отрицательно, а μ положительно, то x_rr<0.

(3) Выражение

0U_r+ u₁U_1r+ u₂U_2r+....+ u_nU_nr

образует определитель, у которого две строки одинаковы; следовательно, оно равно нулю. Но так как u_sU_rs=p_sμUx_rs=p_sUx_rs, то из этого соотношения можно вывести соотношения между х, а именно

.

Следовательно, Σp_sX_rs (по всем значениям s, кроме r) = -р_rХ_rr. которое несомненно положительно.

(4) В нашей работе до сих пор использовались лишь два условия стабильности из всего их набора (4.1), при­чем эти два условия мы свели к одному условию, соглас­но которому U_rr/U отрицательно. Что означают остальные условия стабильности? Пойдем дальше, чтобы ответить на этот вопрос.

Пусть U_{11, 22}-алгебраическое дополнение u₂₂ в U₁₁; U_{11, 22, 33}-алгебраическое дополнение u₃₃ в U_{11, 22}; и т. д. Тогда условия стабильности говорят о том, что

отрицательны и положительны попеременно.

Из хорошо известного свойства обратных определите­лей [См., например: Вurnside and Pantоn, II, р. 42.] следует, что

будут отрицательными и положительными попеременно.

Но это условие того, что квадратичная форма вида

отрицательна для всех значений z. (См. выше.) Помимо прочих значений, z могут оказаться равными u. Следо­вательно,

Итак,

для всех значений m, меньших n.

Таким образом, мы получили четыре правила, кото­рым должны подчиняться члены уравнения, выражаю­щие действие эффекта замещения:

для всех значений m, меньших n.

Из второго и третьего правил, взятых вместе, следует, что

а из третьего и четвертого, взятых вместе, - что

Это шестое правило можно выразить и следующим об­разом. Если разделить n товаров на две группы любым возможным способом и образовать выражение p_rp_sx_rs (здесь x_r берется из одной группы, а x_s - из другой), то Σ Σp_rp_sx_rs (где r и s пробегают все возможные значе­ния в своих группах) должно быть положительным.

Насколько я понимаю, это единственно важные пра­вила, которым должно соответствовать количество това­ров, приобретенных потребителем на доход. Можно заме­тить, что правило (2) является частным случаем прави­ла (4), а правило (5)-частным случаем правила (6).

9. Дополняемость. Как и в самом тексте книги, я бу­ду говорить, что два блага X_r и х_s являются взаимо­заменяемыми с точки зрения определенного потребителя, если для него x_rs>0, и взаимодополняемыми, если для него X_rs<0. Из правила (5) сразу следует, что хотя и воз­можно, чтобы все прочие потребляемые блага были заменителями Х_r, но невозможно, чтобы все они были допол­няющими по отношению к x_r. А из правила (6) следует, что есть еще одно ограничение на распространенность отношений дополняемости. Существует много способов собрать члены, соответствующие эффекту замеще­ния между парами благ, в группы, внутри которых количество пар взаимозаменяемых товаров должно перевеши­вать количество пар взаимодополняемых товаров. Из группы в n благ можно составить 1/2 n (n-1) различных пар благ; эти 1/2n (n-1) пары можно объединить в груп­пы такого типа

различными способами. 1/2n (n- 1) выражений p_rp_sx_rs (r<>s) не обязаны быть все положительными; но существует 2^n-1-1 различных наборов этих выражении, суммы кото­рых должны быть положительными. Именно в этом смыс­ле заменяемость является доминирующим отношением в системе в целом.

10. Спрос на группу благ. Нам предстоит рассмотреть еще самое важное применение правила (4). Начнем с то­го, что из нашего фундаментального уравнения следует, что стоимость приращения спроса на Х_s, которое вызвано данным пропорциональным изменением цены Х_r, равна

Здесь р_rx_r - объем расходов на товар x_r; p_s (δх_s/δМ) оп­ределяет приращение расходов на товар x_s, которое было бы вызвано увеличением дохода потребителя.

Предположим теперь, что цены группы благ x₁, x₂, ... x_m (ms (s

Стоимость приращения спроса на всю группу благ опре­деляется дальнейшим суммированием:

Это выражение идентично по форме выражению (10.1); ему можно дать соответствующую интерпретацию. Далее, так как г и s суммируются по одной и той же группе товаров, то из правила (4) следует, что член уравнения, соответствующий эффекту замещения в (10.2), обязательно будет отрицательным.

Таким образом, мы математически показали очень важный принцип, часто используемый в самой книге, что, если цены на группу благ изменяются в одной и той же пропорции, эту группу благ можно рассматривать точно так же, как если бы речь шла о единичном товаре.

11. Предложение товаров. Предположим теперь, что индивид выходит на рынок не с данной суммой денег (ко­торая не меняется при изменении цен), а с определенным количеством товара на продажу, так что сумма, которую он сам может израсходовать, зависит от уровня рыноч­ных цен. Чтобы рассмотреть общий случай, предположим, что вначале у него имеется n товаров в количестве x₁, x₂, ..., x_n каждый. В результате торговли он будет увеличивать или уменьшать эти количества таким образом, чтобы получить, как говорилось прежде, предпочитаемый им набор благ х₁, x₂, ..., х_n. Первое из условий равнове­сия (6.1) примет тогда следующий вид:

Это единственное изменение, которое необходимо внести в данную систему.

Оно сводится к замене М на Σ p_rx (cp)_r, последняя вели­чина теперь зависит от уровня цен. Следовательно, диф­ференцируя уравнения, мы не можем больше считать, что δМ/δр_r=0, а должны утверждать, что δМ/δр_r=x (ср)_r. Первое уравнение из (7.1) приобретает тогда вид:

Вместо уравнения (8.1) получим:

Это уравнение отличается от нашего исходного фунда­ментального уравнения только тем, что его член, соответ­ствующий эффекту дохода, взвешивается чистым прира­щением блага x_r.

12. Рыночный спрос. Одно из самых очевидных до­стоинств нашего фундаментального уравнения заключа­ется в том, что его можно использовать непосредственно для изучения воздействия, которое изменение цепы ока­зывает на спрос со стороны группы индивидов. Если сум­мирование производится по всем членам группы, то полу­чаем:

Член уравнения, соответствующий эффекту дохода, отра­жает воздействие, которое оказывает на спрос со сторо­ны группы индивидов на товар х увеличение их дохода, если общий прирост дохода распределяется между пред­ставителями группы пропорционально их предшествующему чистому спросу на товар x_r. Член уравнения, соответ­ствующий эффекту замещения, является просто суммой «индивидуальных» членов, соответствующих эффекту за­мещения; следовательно, он должен определяться по тем же правилам, по которым определяются его составные части. Если записать член уравнения, соответствующий эффекту замещения для группы индивидов Σx_rs в виде X_rs, то получим совершенно аналогичные правила:

Приложение к главе IV

13. Равновесие обмена. Здесь необходимо лишь выра­зить классические рассуждения Вальраса в наших собст­венных терминах.

Есть N индивидов, которые выносят на рынок в раз­личных количествах n товаров и обмениваются ими в ус­ловиях совершенной конкуренции. Так как мы обозна­чаем количество r-го товара, находящееся первоначально у представительного индивида, через x (ср)_r, а количество товара, которое он оставит у себя после окончания тор­говли, через x_r (x_r>x (ср)_r, если он является покупателем то­вара и x_rr, если он является продавцом), то обозначим общее количество товара, представленного на рынке все­ми индивидами вместе, через X (ср)_r, а количество товара, которое у них останется - через X (ср)_r.

Цены n товаров будем обозначать, как и прежде: p₁, р₂, ..., р_n. Но необходимо помнить, что один из товаров (например, x_n) придется принять за масштаб стоимости. Таким образом, р_n=1. Остальные цены (p₁, р₂, ..., p_n-1) должны быть определены.

Если система будет находиться в равновесии, то спрос на каждый товар должен равняться его предложению. Следовательно,

Х_r=Х_r (r= 1, 2, 3,..., n). (13.1)

Тем самым мы получаем n уравнений, соответствую­щих n товарам; но нам предстоит определить только n-1 цен. Одно уравнение, однако, служит следствием всех остальных. Среди уравнений равновесия для репрезента­тивного индивида есть такое:

Суммируя эти уравнения по всем индивидам, получим:

Последнее уравнение должно выполняться всегда, неза­висимо от того, выполнятся ли уравнения (13.1). Следовательно, если n-1 уравнение (13.1) выполняется, то должно выполняться и n-е уравнение. Таким обра­зом, у нас есть n-1 уравнение для определения n-1 цены.

Приложение к главе V

14. Стабильность равновесия обмена. Так как значения Х_г можно считать постоянными, то условия стабильности обмена можно получить из анализа знака dX_r/dp_r. Чтобы равновесие было совершенно стабильным, dX_r/dp_r должно быть отрицательным.

(1) если цены всех прочих, кроме данного, товаров не изменяются,

(2) если p_s приводится в соответствие с другими цена­ми таким образом, что на рынке x_s поддерживается рав­новесие, а цены остальных товаров не меняются.

(3) если p_s и p_t применяются аналогичным образом и т. д., пока не будут изменены соответствующим образом все цены, за исключением р_r (и, конечно, р_n , которая обя­зательно равна 1).

Так, третье из этих условий предполагает, что dX_r/dp_r отрицательно, если

Избавившись от dp_s/dp_r и dp_t/dp_r, получим

Так мы получим одно из выражений, которое должно быть отрицательным, чтобы система оказалась стабиль­ной.

Если рассмотреть все такие условия вместе и учесть, что они должны выполняться для рынка каждого из то­варов x_r (r=1, 2, 3, ..., n-1), то условиям стабильности можно придать более удобную форму. Необходимо, что­бы якобианы

(для всех значений r, s, t в диапазоне 1, 2, 3, ..., n-1) были отрицательны и положительны попеременно.

15. Мы знаем, что

Таким образом, когда Х_rr отрицательно, условия стабиль­ности первого порядка могут не выполняться только в том случае, если значение члена, соответствующего эф­фекту дохода в приведенном выше выражении, велико и положительно. Но если приведенную выше формулу применить к группе индивидов (ко всему рынку в целом, т. е. к продавцам и покупателям вместе), то член урав­нения, соответствующий эффекту дохода, обнаружит одно своеобразное свойство. Если количество товара δх_r/δМ (т. е. приращение x_r), которое будет куплено в резуль­тате данного повышения дохода, окажется одинаковым для всех агентов рынка, то член уравнения, соответствую­щий эффекту дохода, примет вид: (Х (ср) _r-Х_r) (δх_r/δМ). Так как для состояния равновесия Х_r=Х (ср) _r, то член уравнения, соответствующий эффекту дохода, будет равен нулю. Сле­довательно, значение члена уравнения, соответствующего эффекту дохода, будет велико, когда покупатели и про­давцы реагируют на изменение в уровне дохода совер­шенно неодинаково. Его значение велико и положитель­но в том случае, когда продавцы склонны по мере того, как становятся богаче, увеличивать потребление товара Х _r гораздо больше, чем покупатели этого товара в тех же самых обстоятельствах.

Таким образом, подобное значительное различие в поведении покупателей и продавцов является одной из воз­можных причин нарушения стабильности. Чтобы выяс­нить, могут ли существовать какие-либо другие причи­ны, предположим, что подобного несоответствия нет ни на одном рынке, так что всеми членами уравнения, со­ответствующими эффекту дохода, можно пренебречь.

Якобианы устойчивости сводятся тогда к следующему виду:

Про эти определители мы знаем, что первый из них отри­цателен. Чтобы рассмотреть определитель второго поряд­ка, преобразуем его, используя правило (3). Будет удоб­но предположить, что все прочие товары, за исключением Х_m и X_s, сгруппированы вместе в составной товар Х₀ (мы имеем право это делать, так как данный определитель второго порядка возникает из рассмотрения случаев, ког­да цены прочих, кроме данного, товаров предполагаются заданными). Используя правило (3) в форме

получим второе условие нестабильности в виде следую­щего выражения:

Очевидно, что это условие будет удовлетворяться, если все три пары товаров будут взаимозаменяемы; оно будет также выполняться, даже если в системе присутствует определенная дополняемость, при условии, что масштабы этой дополняемости не слишком велики.

Нетрудно с помощью метода индукции показать, что условия и более высокого порядка могут быть представ­лены аналогичным образом. Следовательно, наши рассуж­дения сохранят силу и здесь.

16. Последствия расширения спроса. Предположим, что спрос на товар x_r немного увеличится. С этим вопро­сом можно разобраться, как мы делали (см. гл.V), выяснив, какие изменения цен были бы необходимы в ста­рых условиях, чтобы вызвать на рынке товара x_r малое превышение предложения над спросом, если предложе­ние остается равным спросу на рынках прочих товаров (за исключением рынка товара x_n, принятого за единицу масштаба стоимости, так как спрос на x_r расширился за счет спроса на товар x_n).

Из условий стабильности с очевидностью следует, что следует предполагать повышение цены товара x_r.

Каким будет воздействие на цены прочих товаров, можно понять из анализа уравнений (14.1). Предполо­жим вначале, что влияние повышения цены x_r на все прочие цены, за исключением цены товара x_s, достаточно мало и его можно не рассматривать. Тогда из второго уравнения (14.1) получаем:

следовательно,

(если членами уравнений, соответствующими эффекту дохода, можно пренебречь). Так как x_ss отрицательно, то цена товара x_s увеличится, если товары x_s и x_r взаимоза­меняемы, и уменьшится, если они взаимодополняемы.

Если переписать эту формулу в виде:

(мы использовали правило (3)), то p_s увеличится по срав­нению с р_r в меньшей степени, за исключением случаев, когда x_s и x₀ находятся в отношении дополняемости).

Далее, предположим, что цены товаров х_s, и x_t могут существенно измениться. Тогда из второго и третьего уравнений (14.1) имеем:

(членами уравнений, соответствующими эффекту дохо­да, мы пренебрегаем). В этом выражении знаменатель положителен, что следует из условий стабильности. Первый член числителя означает, что есть прямое воздейст­вие на цену товара x_s, второй член свидетельствует о опо­средованном воздействии на цену x_s через цену x_t. Если товар x_t не взаимосвязан с х_r и x_s, то значение последнего члена будет, как правило, пренебрежимо мало, а форму­ла сведется к более простому виду (см. 16.1). Но если между товарами наблюдается тесная взаимосвязь, то кос­венное воздействие повышения цены xr будет осущест­вляться в соответствии с правилом «замещения взаимо­заменяемых товаров (см. гл. V).

17. Возьмем последний якобиан из всего набора опре­делителей стабильности-тот, у которого n-1 строк и столбцов, так что он включает в себя все товары, за ис­ключением товара, принятого за единицу масштаба стои­мости, и все переменные цены. Назовем его I. Пусть I_rr, I_rs - алгебраические дополнения δХ_r/δр_r, δХ_r/δр_s в I. Пусть I_{rr, ss}, I_{rr, st} - алгебраические дополнения δХ_s/δр_s, δХ_s/δр_t в I_rr.

Тогда, учитывая косвенное воздействие повышения цены x_r через цены всех прочих товаров, получаем (см. 14.1):

Если, пренебрегая эффектом дохода, мы уберем все элементы Х_rr, Х_ss и т. д. при помощи третьего правила, то полученное уравнение можно рассматривать как «пре­образование» dX_r/dp_r в понятия эффектов замещения, дей­ствующих между парами товаров Х_rs, Х_st, где r<>s<>t. Что можно сказать о зависимости уравнения от этих эффек­тов замещения?

Дифференцируя (17.1) по Х_st, где или s, или t (но, как очевидно, не оба вместе) может равняться r, получим:

Из нашего третьего правила следует, что δx_ss/δx_st = -p_t/p_s, а из хорошо известного свойства обратных определителей - что

Используя эти свойства, мы можем продолжить диффе­ренцирование

что означает обязательный отрицательный результат. dX_r/dp_r неизбежно отрицательно; следовательно, мы до­казали, что абсолютная величина этого выражения будет тем больше, чем больше эффект замещения между лю­бой парой товаров в системе.

Приложение к главе VI

18. Равновесие фирмы. Условия равновесия. Можно считать, что фирма использует различные количества факторов y₁, у₂, у₃, ..., y_m для производства различных ко­личеств продуктов x_m+1, x_m+2, ..., x_n. Ее цель состоит в максимизации прибыли:

при условии, что выполняется соотношение, связывающее х и у. Так как с точки зрения фирмы разница между фактором и продуктом-всего лишь разница в знаке, то для простоты мы можем рассматривать факторы как отрицательные продукты, обозначив -y_r через x_r (r

при соблюдении условия f(x₁, x₂, х₃, ..., x_n)=0. (Необхо­димо отметить, что функция f произвольна в том же са­мом смысле, в каком была произвольна функция полезно­сти u. Любая функция φ (f), которая равна 0, когда f рав­на 0, годится для анализа наравне с f.)

Если предположить, что фирма находится в условиях совершенной конкуренции, то задачу максимизации можно опять исследовать путем введения множителя Лагранжа и максимизации выражения V-μ f. Отсюда имеем:

d(V-μf)=0

d²(V-μf)<0.

Из первого условия мы получаем: pr=μ f_r {r=1, 2, 3, ... ..., r_e). Если избавиться от μ , то получим n-1 уравнение, которые вместе с производственной функцией опреде­ляют n величин x₁, х₂, ..., Х_n.

Так как V линейна, то d²V=0, следовательно, второе условие предполагает, что d²f>0, если df=0.

Преобразуя полученные выражения (так же как и в § 4, но с учетом разницы в знаке), мы получаем анало­гичный набор условий стабильности. Все определители

должны быть отрицательными. (См. 2(3).)

Будет удобно использовать обозначения, в точности аналогичные тем, которые мы применяли при рассмотре­нии теории полезности. Так, если F - последний из дан­ных определителей, то алгебраическое дополнение f_rs в F будет обозначаться как F_rs. Условие того, что F_rr/μ F поло­жительно, инвариантно относительно замены f на φ (f) в качестве производственной функции.

Приложение к главе VII

19. Равновесие фирмы. Воздействие на него изменения цены. Предположим теперь, что цена рr меняется, а цены всех остальных товаров остаются неизменными.

Уравнения равновесия выглядят следующим образом:

Продифференцируем их по:

Из вида определителей стабильности следует, что вы­ражения F_rs/μ F будут подчиняться законам, очень похо­жим на те, которым подчинялись члены уравнений, соот­ветствовавшие эффекту замещения в теории полезности. Если один раз изменить знак, то эти правила можно сде­лать идентичными. Поэтому обозначим:

Соответственно, получим наше фундаментальное уравне­ние в виде

и в точности аналогичный набор правил:

Фундаментальное уравнение записано в такой форме, в которой оно выражает воздействие изменения цены (про­дукта или фактора) на предложение продукта. Чтобы вы­яснить, каким будет воздействие на величину спроса на фактор, необходимо лишь заменить x_s на -y_s. Фундаментальное уравнение будет тогда выглядеть следующим образом: σy_s / σp_r = х_rs. Наши правила остаются совершенно без изменений.

20. Тенденция к преобладанию отношений дополняе­мости между факторами. В теории производства, разра­ботанной в двух предыдущих разделах, неявно предпола­гается, что предприниматель обладает некоторым фикси­рованным производственным ресурсом, который ограни­чивает размеры производства и по отношению к которому прибыль V может считаться доходом. Если такого фик­сированного ресурса не существует, то у нас нет основа­ний считать, что одинаковое пропорциональное увеличе­ние всех факторов не позволит увеличить производство всех продуктов в соответствующей пропорции. С матема­тической точки зрения это будет означать, что если f (x₁,x₂,..., x_n)=0

то f(λx₁, λх₂, ..., λх_n)=0

для всех значений λ. Производственная функция (запи­санная, как мы ее писали, в неявной форме) будет одно­родной функцией нулевого порядка.

Тогда, по теореме Эйлера, Σx_rf_r=0. (Так как из 19.1 следует: pr=μf_r, предполагается, что V=0.) Дифференцируя еще раз, получим f_s+ Σ x_rf_r, s=0 (s=l, 2, 3, ..., n).

Если использовать эти тождества для преобразования определителей стабильности, то сразу станет ясно (мы умножаем 2-ой, 3-ий, ... столбцы на х₁, х₂... и складываем их с первым), что F (последний из определителей устой­чивости) равен нулю.

Так как х'_rs=- F_rs/μ F, все члены х' обращаются в беско­нечность. Цена одного фактора (или продукта) не может измениться, если не меняются цены других факторов или продуктов, чтобы равновесие не оказалось полностью на­рушенным. Если цена продукта растет, объем производ­ства будет бесконечно большим; если же цена фактора растет, его значение станет равным нулю. Для того край­него случая, который мы рассматриваем наш анализ мо­жет оказаться совсем непригодным.

Тем не менее полезно выяснить, чем определяется на­правление изменения предложения продуктов или спро­са на факторы, так как можно ожидать, что соответст­вующие законы будут верны и тогда, когда мы будем приближаться к рассмотрению крайнего случая, не до­стигая его. Для ответа на этот вопрос можно вычислить F_rs, при условии, что производственная функция однород­на в нулевой степени.

Преобразуя этот определитель дважды тем же методом, который мы использовали для преобразования F, полу­чим, что он равен x_rx_sF₀, где F₀ - алгебраическое допол­нение 0 в определителе F, т. е. главный минор определи­ теля. Следовательно,

x'_rs=-x_rx_s F₀/μ F

для всех значений r и s.

Так как мы знаем, что x'_rr отрицательно, то F₀/μ F должно быть положительным. Если x_r и х_s, оба продук­ты или оба факторы, то x_rx_s будет положительным, a x'_rs, следовательно, отрицательным. Если один из них - про­дукт, а другой - фактор, то x_rx_s отрицательно, a x'_rs, сле­довательно, положительно.

Таким образом, по мере приближения к рассмотре­нию предельного случая, мы должны полагать, что фак­торы и продукты распадутся на две взаимодополняемые группы; в то время как «заменяемость», которая тем не менее должна доминировать в системе в целом (в системе факторов и продуктов, взятых вместе), будет обеспечиваться исключительно отношениями фактор - продукт.

Приложение к главе VIII

21. Общее равновесие производства. Теперь необходи­мо свести воедино все выводы, к которым мы пришли, и использовать их для выяснения вопроса о том, как ра­ботает вся статическая система в целом. Мы предполагаем (как и в тексте книги), что индивиды, составляющие эко­номическую систему, представляют на рынок один (или оба) из ресурсов двух видов: (1) товары или факторы, которые можно непосредственно продавать на рынке, (2) «предпринимательские» ресурсы, которые можно ис­пользовать для производства товаров на обмен, но которые сами по себе не могут быть проданы. При любой данной системе цен будут использоваться только те предприни­мательские ресурсы, использование которых принесет по­ложительную прибыль.

При данной системе цен будет наблюдаться опреде­ленный спрос на товары со стороны потребителей (со­вокупный потребительский спрос на товар Х_r мы обозна­чим как Х_r); будет наблюдаться предложение непосред­ственно от частных лиц (X_r); и будет наблюдаться пред­ложение только что произведенных товаров (Х'_r). Рынок товара Х_r будет находиться в равновесии, если

Х_r=Х(ср) _r+Х'_r. (21.1)

Необходимо отметить, что это уравнение записано и самом общем виде; оно может использоваться по отноше­нию к товару, услуге, продукту или фактору. Если Х_r - товар конечного потребления, предложение которого це­ликом обусловлено производством, то Х_r=0 и уравнение приобретает вид:

X_r=X'_r

Если этот фактор производства (такой как труд), то Х'_r отрицательно. Х_г включает в себя спрос па прямые услу­ги фактора, независимо от того, предъявляется он другими людьми или самим поставщиком фактора. (Это, видимо, самый удобный способ учитывать изменения в предложе­нии фактора). Таким образом, уравнение выглядит сле­дующим образом:

(-Х'_r)+Х_r =Х(ср) _r.

Если Х_r - полуфабрикат, который производится и потреб­ляется в ходе производства, но продается одной фирмой другой фирме, то только по этой причине X, и Х(ср)=0 и уравнение принимает вид: x'_r=0.

(Чистое предложение всех фирм, взятых вместе, равно нулю.)

Таким образом, уравнение одного и того же вида под­ходит для всех товаров и услуг. Как и прежде, один из товаров должен служить масштабом измерения стоимо­сти; так что если имеется всего n товаров, то необходи­мо определить n-1 цен. Как и прежде, одно уравнение следует из остальных. Среди уравнений, задающих усло­вия равновесия частного лица, имеется следующее:

где V - прибыль, которую оно получает от обладания каким-либо предпринимательским ресурсом. Суммируя ато по всем индивидам, получаем:

где Σ V - общая сумма прибыли для всей экономики. Аналогично, для каждой фирмы:

Σ p_rx_r =V

Суммируя эти уравнения, получаем:

следовательно:

Таким образом, если уравнения равновесия (21.1) вы­полняются для n-1 товаров, то они должны выполнять­ся и для n-го товара. Есть только n-1 независимое уравнение, и система не является переопределенной.

22. Стабильность общего равновесия. Как и в равно­весии обмена, для обеспечения стабильности необходимо, чтобы падение цены на любом рынке делало спрос боль­шим, чем предложение. Чтобы стабильность была совер­шенной, это условие должно выполняться, если (1) .цены всех прочих товаров постоянны, (2) цены меняются одна за другой таким образом, чтобы поддерживалось равно­весие на остальных рынках. Для несовершенной стабиль­ности необходимо, чтобы это условие выполнялось и пос­ле изменения всех прочих цен.

Данное условие можно записать в виде: d/dp_r (X_r-X_r-x'_r) < 0. Но так как Xr можно считать заданным неза­висимо от уровня цен, оно сводится к выражению:

Это выражение можно раскрыть, как и в разделе 14. Оно превратится в отношение двух определителей, типичный элемент которых будет выглядеть как

Мы знаем, как преобразовать последнее выражение. Из (12.1) следует:

(с учетом изменения V при изменении p_r).

Из (19.4) следует, что δx_s/δp_r=-x'_rs для каждой фирмы; таким образом, суммируя, мы получим δX_s/δp_r=-X'_rs, где X'_rs должно изменяться как и X_rs.

Следовательно, δ/ δp_r (X_s-X'_s)= Σ (x(ср) _r+x'_r-x_r) δx_s/δM+ X_rs+X'_rs. Так как движение X_rs и X'_rs подчиняется од­ним и тем же правилам, то и движение X_rs+X'_rs должно подчиняться тем же правилам.

Таким образом, выражение δ/ δp_r (X_s-X'_s) изменяется так же, как и выражение δx_s/δp_r, которое мы рассматривали в теории обмена. Следовательно, дальнейший анализ общего равновесия производства совпадает с анализом общего равновесия обмена; все выводы разделов 15-17 можно интерпретировать в более широком смысле.

Приложение к главе XV.

23. Определение плана производства. Продолжим рас­сматривать факторы как отрицательные продукты, как это было удобно делать в теории статики. В динамике задача, стоящая перед фирмой, заключается в том, чтобы определить поток выпускаемых продуктов, который может быть произведен на имеющемся оборудовании и который будет обладать максимальной дисконтированной стоимо­стью (см. гл. XV). Если мы обозначим через x_r0, x_r1,..., x_rv количества товара x_r, которые планируется продавать в каждую последующую «неделю», начиная с нынешней, то производственная функция примет вид f(x₁₀, x₂₀, ..., Х_n0, х₁₁, х₂₁, ..., x_n1, x₁₂, x₂₂, ..., х_n2, ..., x_1v, x_2v, ..., x_nv) =0, если считать, что план распространяется вперед на v недель.

Дисконтированная стоимость плана равна

где Βt=l/(l+i_t), a i_t-ставка процента (в неделю) для ссуд сроком на t недель; р_ro - текущая цена x_r и p_rt - цена, которая, как считает предприниматель, установится через t недель. (Необходимо считать, что в prt учитывает­ся риск таким образом, как это описано в тексте в гл. XV, раздел 6.)

С точки зрения индивидуального предпринимателя, в условиях совершенной конкуренции все бета и все р заданы; следовательно, несмотря на то, что эта задача кажется более сложной, с формальной точки зрения она тождест­венна задаче, рассмотренной в разделе 18. Нет не­обходимости выписывать полностью условия равновесия. Законы, показывающие, каким образом будет устанавли­ваться соответствие между планом производства и фак­тическими или ожидаемыми ценами, аналогичны тем, ко­торые получены в разделе 19. Но при записи шести пра­вил, которым должны удовлетворять члены уравнения, соответствующие эффекту замещения, мы должны не за­быть заменить p_r на Β ^t_tp _rt и провести суммирование не только по всем r, но и по всем t.

Приложение к главе XVII

24. Воздействие процента на план производства. Изу­чая воздействие изменений процента на план (при условии, что цены и ценовые ожидания заданы), удобно вос­пользоваться тем свойством, что все продукты, для кото­рых дисконтированные отношения цен в рамках данной задачи можно считать заданными, можно рассматривать как один продукт. Следовательно, мы можем теперь не различать типы продуктов (и факторов), планируемых на определенную неделю, а также отказаться от учета в на­ших формулах цен в явном виде. Начиная с данного мо­мента X_t будет обозначать ожидаемую денежную оценку всех факторов и продуктов, взятых вместе, которые пла­нируются на неделю, начинающуюся через t недель - иными словами, прибыль, планируемую на рассматривае­мую неделю.

Приняв это упрощение, можно сказать, что предпри­ниматель стремится максимизировать

при условии, что f(x₀, x₁, .... х_v) =0.

Воздействие на прибыль x_t изменения ставки процента по ссудам на t' недель будет задаваться выражением

в то время как среди шести правил, которым должны подчиняться х, имеется правило (3), согласно которому

Чтобы выяснить, каким будет воздействие на при­быль x_t общего изменения процентных ставок, обратим внимание на то, что

и, следовательно,

Таким образом, если дисконтирующие отношения (Р) для ссуд на все периоды изменяются в одинаковой пропор­ции, то соответствующее воздействие на x_t определяется выражением:

если ставки процента в неделю для ссуд на все периоды равны и таким образом дисконтирующие множители так­же равны.

Используя (24.1), это выражение можно записать в виде:

Если последнее выражение выписать полностью, станет ясно, что его член с х'_tt равен нулю. Но именно х'_tt в со­ответствии с правилом (2) должен быть непременно от­рицательным; если взаимодополняемости нет, то все ос­тальные x'_tt будут положительными. Это означает, что если ставка процента падает (р растет), то будет наблю­даться замещение всех прибылей, получаемых прежде x_t, прибылью x_t, и замещение прибыли x_t всеми прибыля­ми, получаемыми позднее x_t. Это обычное правило, на дело может осложняться при существовании дополняе­мости.

25. Средний период плана. Как и в главе XVII, мы определяем соответствующий средний период следующим: образом:

следовательно,

Дифференцируя по р, но считая р' постоянным в соответ­ствии с известным правилом, получим:

следовательно,

(так как если А=В, то они оба равны - (А+В).)

В последнем выражении опять все члены с t=t' авто­матически можно считать равными нулю. Следовательно, если дополняемости нет, все оставшиеся х'_tt' будут положительными, и все выражение окажется положи­тельным. Падение ставки процента должно увеличи­вать продолжительность среднего периода плана. Даже если есть отношения дополняемости, остается шестое пра­вило, согласно которому Σ Σ Β^t+t'x_tt' >0 при t<>t'; сле­довательно, dP/dΒ может быть отрицательным, только если дополняющие пары таковы, что (t-t')² для них велико. Это означает, что взаимодополняемые значения прибыли находятся на противоположных концах плана. Я думаю, что этот случай можно рассматривать только в качестве любопытного исключения.
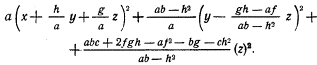
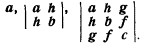
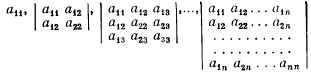
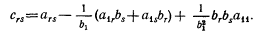
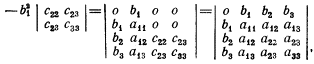
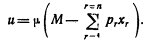
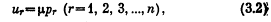
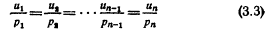
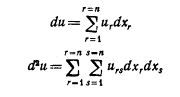
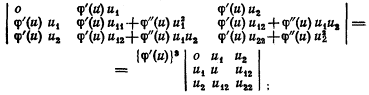
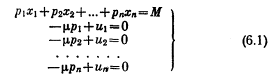
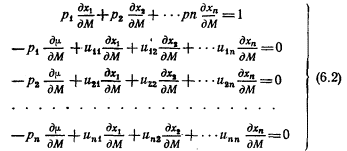
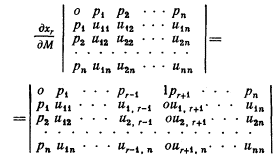
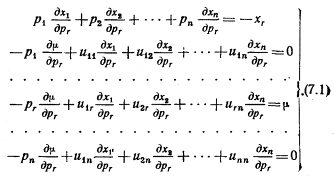
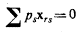